1.4 计算
1.4.1 方法
1. 极限四则运算规则
若
①
②
③
【注】(1) 若
存在, 不存在,则 必不存在. ( 。 加法中,有任何一部分极限存在,则可直接拆分. ) (2) 若
不存在, 也不存在,则 不一定不存在. (3) 若
,则 ,即乘除法中非零因子可往外先提出去.
【例 1.20 】证明: (1) 若
(2) 若
证明 (1) 由于
(2) 由于
【注】以上结论非常重要, 以后在有关定参数的题目中可直接使用, 如下例.
【例 1.21】 设
(A) -4 (B) -3 (C) -2 (D) -1
解 应选 (A).
2. 洛必达法则
法则一 设① 当
②
③
法则二 设①当
②
③
【注】(1) 一般来说,洛必达法则是用来计算 “
” 型或者 “ ” 型未定式的,不是 “ ” 型和 “ ” 型, 就不能用洛必达法则. (2) 如果极限
仍属于 “ ” 型或者 “ ” 型,且 继续满足洛必达法则的条件,则可以继续使用洛必达法则,即 . (3) 如果
不存在也不为 ,不能推出 不存在也不为 ,简单一点说就是: 对于
,“ 右存在,则左存在; 但左存在,并不意味着右一定存在 ”. 比如说,极限 存在, 而如果使用洛必达法则, 会有
这个极限显然不存在. 这是一个很细致、很隐蔽的问题, 稍不注意就可能出错.
【例 1.22】 证明:
(1) 当
(2) 当
证明 (1) 由于
(2) 当
【例 1.23】 设
(A)
(B)
(C)
(D)
解 应选 (C).
因为
故选项 (C) 正确.
【注】① 当
时,有 ,其中 ,符号 “ ” 叫远远小于; ② 当
时,有 ,其中 .
3. 泰勒公式
设
如
再如
同理可得如下重要函数的泰勒公式.
【注】从数学命题的角度对以上公式进行处理, 可得到一组 “差函数” 的等价无穷小代换式, 如
,则 ,同理有 等,并可将这些公式广义化,如第一个公式广义化为狗
狗 (狗) (狗 ),其余类似.
4. 无穷小的运算
设
①
②
③
【注】在后面泰勒公式的应用中, 会对上述高阶无穷小的运算提出要求, 请读者学会正确书写
5. 泰勒公式应用时的展开原则
(1)
具体说来,如果分母 (或分子) 是
例如,计算
由于
因此
这里顺便得到了一个重要的等价代换式
同理
均可由 “上下同阶” 原则得到.
(2)
具体说来,即将
例如,已知当
用泰勒公式,
显然,将
行运算, 得
于是可知
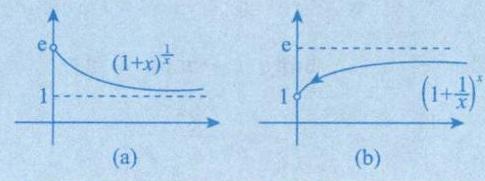
6. 两个重要极限
【注】常考变量广义化
如狗
,则上述式子为
7. 夹逼准则
如果函数
(1)
(2)
则
【注】常见的一个问题: 设任意的
,总有 ,且 ,则 是否一定存在? 答案是否定的. 存在并不能说明 都存在, 从而也不能保证 存在. 例如,当
时,取 ,则 ,且 ,但 不存在.
1.4.2 七种未定式的计算
考研的函数极限计算题一般归纳为七种未定式:
题型: 直接计算、反求参数、已知某一极限求另一极限、无穷小的比阶等.
解题思路如下:
①化简先行.
a. 提出极限不为 0 的因式; b. 等价无穷小代换; c. 恒等变形 (基本的恒等变形法如提公因式、拆项、 合并、分子分母同除变量的最高次幂等, 高级的恒等变形法如变量代换, 也叫换元法等). 需要强调的是, 很多问题如果不化简就计算, 可能计算会很复杂, 甚至可能计算不出结果.
②判断类型 (运算类型).
③选择方法 (洛必达法则、泰勒公式、夹逼准则等).
(1) “
【例 1.24】
解 应填
原极限
【注】
在 时有以下性质: ①
单调减少; ② ; ③ .
【例 1.2】 求极限
解 若
若
若
综上,
【注】本题的结果要记住,以后直接使用,这就是通常说的 “抓大头”,即当
时,分别抓分子、 分母中关于 的最高次项,忽略其他项,如 . 另外特别注意,若 ,则应该分别抓分子、分母中关于 的最低次项.
【例 1.26】 设函数
解 应填
当
当
综上,
【例 1.27】 已知极限
(A)
解 应选 (D).
方法一 脱帽法.
则
故
方法二 泰勒展开. 由
故
【例 1.28】 求极限
解 这是 “
于是在考研中常考的一个式子是
【注】事实上,当
时, ,本题中 .
【例 1.29】 求
解 当
法——比如等价无穷小代换、泰勒公式、洛必达法则——无法使用时, 一定要能够想得起这个“两边夹击” 的重要方法).
根据
于是
可见,无论
(2) "
【注】对于 “
” 型未定式,一般有两种思路. (1) 如果函数中有分母, 则通分, 将加减法变形为乘除法, 以便于使用其他计算工具 (比如洛必达法则), 见例 1.30 .
(2) 如果函数中没有分母, 则可以通过提取公因式或者作倒代换, 出现分母后, 再利用通分等恒等变形的方法, 将加减法变形为乘除法, 见例 1.31.
【例 1.30】 极限
(A) 2 (B)
解 应选 (D).
所给极限为 “
故选 (D).
【例 1.31】 求极限
解
(3) “
【例 1.32】 求极限
解 这是 “
将其化成 “
因为
(4) “
【例 1.33】 求极限
解 这是 “ 1 ” 型未定式,是幂指函数的极限,如果
推导如下: 利用第二重要极限公式
故 原式
(5) 泰勒公式
【例 1.34】 设当
(A)
(B)
(C)
(D)
解 应选 (A).
方法一 由泰勒公式可知
由题设可知
即
则
方法二 由洛必达法则可知
若
故
【例 1.35】 设函数
(A)
(A)
(C)
(D)
解 应选 (A).
方法一 由于在
因此
又由题设知,在
所以
故选 (A).
方法二 由题设可得在
所以
故
又因为
故
故选 (A).